Explainable AI & Interpretable ML

1. 개요

Interpretability : 모델의 예측 이유(원인)에 대해서 사람이 이해 가능한 단계

Explainability : 각 Feature가 하나의 예측에 대해서 어떠한 기여를 하였는지 확인 가능한 단계

DL 모델이 높은 정확도는 가져올 수 있지만 ML 모델에 비해서 해석력이 낮다.

 

2. Interpretable ML

• Generalized Linear Models
• Generalized Additive Models
• Naive Bayes Classifier
• K-nearest Neighbor Methods
• Explainable Boosting Machines(EBMs)

2.1 선형회귀에서의 해석력(Linear Regression Interpretation)

2.1.1데이터 타입에 따른 해석방법

수치형 데이터(Numerical Feature) : 최소 단위만큼 변화시키면 결과가 얼마나 변하는지

이진 데이터(Binary Feature) : 0일때와 1일때의 차이가 얼마나 나는지(0에서 1로 변환하면 결과가 얼마나 변하는지)

범주형 데이터(Categorical Feature) : 각 범주값이 해당되거나(1) 해당되지 않을때(0) 차이가 얼마나 나는지(0에서 1로 변환하면 결과가 얼마나 변하는지)

Intercept : 

2.1.2 예측 결과 해석

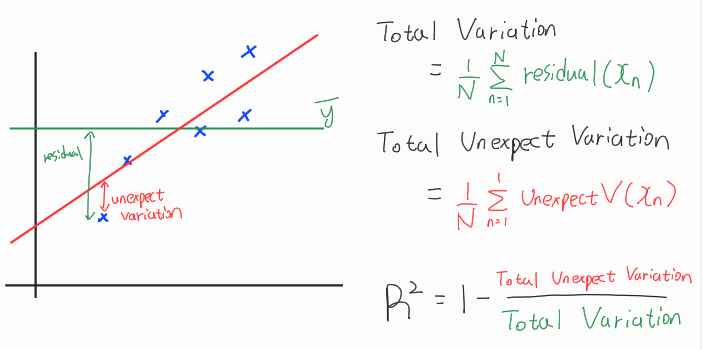
R-Squared(R2, 결정계수)

독립변수(Feature)들이 종속변수에 대해서 어느정도 설명하는지에 대한 지표. (0~1범위의 값을 가지며 1일경우 정확히 설명한다는 의미)

결과값의 변화량(Variation of a dependent variable)이 입력값의 변화량(Independent variables)으로 얼마나 잘 설명되고 있는지.

Regression 문제에서 대표적인 평가지표로 사용된다.

독립변수의 개수가 늘어날수록 R-squared 값이 높아진다는 점을 주의해야한다.(이를 보완하기 위해 Adjusted R-Squared 등장)

 

Adjusted R-Squared(Adjusted R2, 조정결정계수)

기존의 R-squared에서 독립변수의 수와 데이터의 수에 따라서 조정을 거친 지표

N : 데이터 개수

D : 독립변수 개수

선형 모델에서의 Feature Importance(Feature Importance in Linear Model)

직관적으로 독립변수의 영향력은 가중치\((\theta)\)의 값으로 판단할 수 있는데,

이를 해당 독립변수의 standard error로 나누어줌으로 정확한 Feature Importance를 얻을 수 있다.

(standard error가 높다는 의미는 해당 값이 아닌 다른 값일 확률이 높다는 의미이다.)

아래 예시에서는 가중치 값이 더 컸지만 standard error가 높을경우 낮은 Feature Importance를 가질 수 있는 상황을 보여준다.

feature에 해당하는 계수의 표준편차(standard error는 추정치의 표준편차 )

자세히 계산하는 방법은 별도로 있음

2.2 의사결정나무에서의 해석력(Decision Tree Interpretation)

 

2.3 Generalized Linear Models(GLM, 일반화 선형모형)

Linear model은 종속변수(y)가 정규분포를 가지는 연속형 변수임을 가정한다.

하지만 어떠한 데이터는 종속변수(y)가 정규분포가 아니거나 범주형 데이터이다.

이러한 경우에는 GLM을 사용할 수 있다.

Target(y)이 정규분포에 근사할 경우(Gaussian) : Linear Model

Target(y)이 정규분포에 근사하지 않을 경우(Non-Gaussian) : Generalized Linear Model

 

대표적인 GLM 모델 : Logistic Refression, Poisson Regression

 

종속변수(y)가 정규분포가 아니거나 범주형 데이터인 경우를 정규분포에 근사시키기 위해서 Link function을 포함한다.

Link function : linear model에서 만들어진 결과(예측값)를 우리가 필요한 response로 변경해주는 것

(logistic의 경우 logistic inverse가 link function이다)

LM과 GLM을 수식으로 나타내면 아래와 같다. (GLM에서는 예측결과에 대해서 link function(g)가 사용되었다.)

분포에 따른 link funcion의 종류는 아래와 같다.

정규분포(Gaussian)의 경우 변경이 필요없기에 단위벡터가 사용된다.

베르누이분포(Bernoulli) 및 포아송분포(Poisson)의 경우 아래의 식과 같은 linkfunction이 사용된다.

베르누이분포의 경우 binary classification 문제를 다루는 logistic regression에 적용 가능하다.

종속변수가 무언가의 개수일 경우 포아송분포를 적용 가능하다.

커피를 몇잔 마셨을까에 대한 예측 문제가 있다고 가정했을 때,

우리는 GLM의 link function으로 log()를 사용할 수 있다.(종속변수가 무언가의 개수일 경우 포아송분포 적용)

2.4 Generalized Additive Models

해석 가능함을 유지하면서 비선형 데이터를 모델링할 수 있는 방법

GLM 보다 강력하지만, Feature별로 transformation(f)를 적용하기에 Feature간의 상호작용(interaction)이 모델링에 학습되지 못한다.

Feature간의 상호작용을 고려해서 fairwise하게 GAM을 만들기도 하며 이를 \(GA^{2}M\)이라고도 부른다.

대표적인 GAM 모델 : pyGAN

2.5 Explainable Boosting Machines(EBMs)

기존의 GAM에서 f()를 학습시키는데 Boosting 기법을 사용한다.

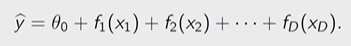
\(GA^{2}M\) 방식을 사용할 경우에도 위와같이 각 Feature에 대해서 Boosting 방법으로 학습 후 지정된 fair에 대해서도 Boosting 방법으로 학습한다.

2.6 Neural Additive Models(NAM)

Additive Models에서 shape function 자리에 Neural Network를 사용한 아이디어

3. Explainable AI

• Model-Specific : 특정 모델에서만 가능한 기법
  • Layerwise Relevance Propagation(LRP)
  • DeepLIFT
• Model-Agnostic : 모델에 상관없이 적용 가능한 기법
  • LIME
  • SHAP
• Counterfactual Explanations

3.1 Layerwise Relevance Propagation(LRP)

Neural Network의 output vertor를 역추적하여 Input vector가 어느정도의 영향력을 미쳤는지 파악하는 기법.

주로 이미지(CNN) 문제에서 많이 사용된다.

아래 그림에서와 같이 고양이 분류 문제가 있다고 가정했을 때 output vector는 [고양이일확률, 고양이가아닐확률] 로 구성되어 있을 것이다. (ex : [0.75,0.25])

타당성 전파(Relevance Propagation)와 분해(Decomposition) 기법을 사용해 output vector부터 모델을 역추적한다.

최종적으로는 input vector의 각 feature들이 어느정도의 기여도를 가지는지 계산한다.

해당 기법에 대한 자세한 설명은 다음 블로그에서 잘 설명하고 있다. (LRP 설명 이동하기)

 

3.2 Interpretable Model-agnostic Explainations(LIME)

복잡한 Black Box 모델을 White Box 모델로 근사화하여 해석하는 방식

전체 데이터가 아닌 구하고자 하는 값의 근방 데이터만을 사용하고,

기존의 복잡한 모델(f)을 단순하고 해석가능한 모델(g)로 근사하며,

g의 복잡도는 낮게 가져간다.

쉽게 말해서 원본 데이터의 값을 단순한 값으로 변환하여서 해석이 용이하게 만든다.

3.2.1 Tabular Data에서의 데이터 변환(해석 가능하게)

Categorical data : 범주의 각 값에 대해서 유무(binary) 형태로 변환한다.

Numerical data : 그대로 사용하거나 구간을 나누어서 범주형으로 변경한다. 

 

3.2.2 Image Data에서의 데이터 변환(해석 가능하게)

아래 그림에서는 원본 이미지를 구간을 나누어서 simplied feature로 변경하였다.

변경된 simplied feature를 통해서 이미지에서 해석하는 방법을 알아보자.

예측모델이 원본이미지가 개구리일 확률(probability)을 54%로 측정했다.

원본 이미지에서 나누어진 component들에 대해서 일부를 랜덤하게 회색으로 변경하여 서브 이미지들을 얻고,

이를 예측 모델에 넣어서 개구리일 확률을 얻는다.

아래 그림에서 첫번째 서브 이미지부터 세번째까지 차례로 85%, 0.001%, 52%를 얻었다.

이때 주목해야할 것은 원본 이미지와 서브 이미지에서의 변경된 확률값과 남아있는 components 그리고 지워진 components이다.

첫번째 서브 이미지에서는 원본대비 확률이 31% 상승했다. 이는 남아있는 component들이 개구리임을 예측하는데 중요한 특징임을 의미한다.

두번째 서브 이미지에서는 원본대비 확률이 약 54% 감소했으므로 남아있는 component들이 개구리 예측에 중요하지 않은 특징임을 의미한다.

 세번째 서브 이미지에서는 원본대비 확률이 2% 감소했으므로 지워진 component들이 개구리 예측에 중요하지 않은 특징임을 의미한다.

이러한 과정들을 통해서 최종적으로 그림 우측 하단의 component가 개구리 예측에 매우 중요한 특징임을 알 수 있다.

위의 예시는 개구리 class에 대해서만 해석한 내용입니다.

실제 예측모델에서는 개구리일 확률 54%, 당구공일 확률 7%, 열기구일 확률 5%로 예측을 수행했습니다.

각 class에 대해서 위의 과정을 수행했을 때 해당 class를 예측하는데 중요한 역할을 한 component들을 뽑아낼 수 있습니다.

 

LIME은 위 과정과 같이 예측 모델의 종류에 종속받지 않는(Model-Agnostic) 기법입니다.

또한 해석하는데 있어서 하나의 데이터만에 대해서 하나의 class만을 대상으로합니다. (문제의 단순화, sampling and local exploration)

 

3.3 SHapley Additive exPlanation

게임이론을 기초로하는 해석기법으로 기여에 따라서 feature들에게 합당한 값을 배분하는 방법이다.

3.3.1 게임이론

특정 유저(feature)에 대한 기여도를 구하기 위해서 아래의 수식을 따른다.

이를 간단한 아이스크림 구매 예시를 통해 설명한다.

철수,영희,길동 세명의 아이가 있고 각각 6,4,3 달러를 가지고 있다.

아이스크림은 s(500g),m(750g),l(1000g)가 있다.

철수의 기여도를 계산하고 싶을 때, 철수에 대한 marginal contribution은 아래와 같다.

(철수가 포함된 집합) - (철수가 빠진 집합)

이때 각 집합의  reward를 계산하면 아래와 같다.

{철수,영희}의 경우 둘의 돈 합이 $10이므로 $9인 아이스크림 M(750g)을 구매 가능하므로,

v(철수,영희)의 reward는 750이다.

이러한 정보로 철수에 대한 기여도를 계산 할 수 있다(우측 하단 노란색 수식)

이때 하나의 세부 예시에 대해서만 계산과정을 살펴본다. (수식에서 i는 철수이다)

예시 대상은 {영희}이다.

대상인 subset은 {영희}이므로 S는 1이다.

D는 전체 player(feature)의 개수로 3이다. (철수,영희,길동)

subset의 reward는 0이며, subset+철수의 reward는 750이다.

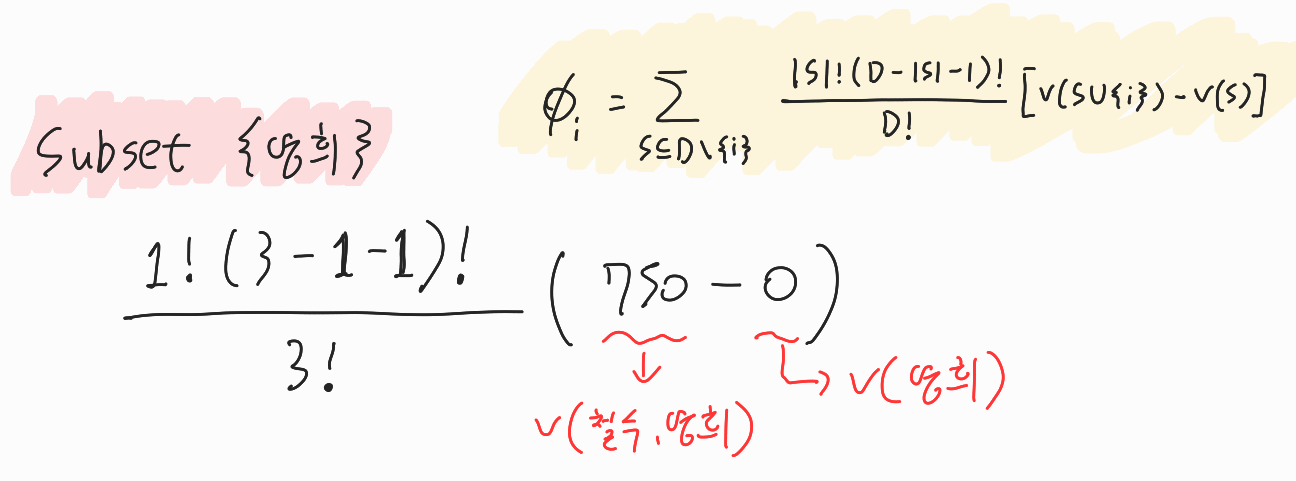
3.3.2 게임이론을 예측모델과 feature에 적용하기

그렇다면 실제 예측모델에서 feature들에 대한 reward는 어떻게 구할 수 있을까?

feature들의 subset을 예측모델에 입력하였을 때 나오는 output이 곧 reward가 된다. (class가 개구리일 확률 58% 등)

하나의 데이터(instance)에 대해서 SHAP 기법을 적용 했을 때 아래와 같은 결과를 얻을 수 있다.

아래의 예시에서는 regression 문제를 다루고 있다.

예측값(y)의 평균은 26.648이다.

feature 'LSTAT'가 5.6의 shap value를 가지며 feature 'RAD'가 -0.9의 shap value를 가진다.

예측값(y)의 평균인 26.648에서부터 예측결과인 22.533이 되기까지 각 feature들이 가지는 기여도는  shap value를 통해 확인 가능하다.

(feature 좌측의 숫자는 실제 데이터가 가지는 값이다.)

 

[XAI/Python] SHAP 파이썬 라이브러리 사용 코드 예시(SHapley Additive exPlanations)

 

이러한 shap value를 계산하는 방법은 여러 종류가 있으며 아래와 같다.

• Model-agnostic approximations
  • Shapley sampling values
  • Kernel SHAP(base on LIME)
• Model-specific approximations
  • Linear SHAP
  • Tree SHAP
  • Deep SHAP

3.4 Counterfactual Explanations

입력 데이터를 일부 변경하였을 때 예측모델의 결과값이 어떻게 바뀌는지.

 

BMI feature를 9 감소시켰더니 예측 결과가 stroke에서 no stroke로 변경되더라.

 

3.4.1 좋은 counterfactual explanation의 조건

• 소수의 feature 변경으로 가능해야한다. (많은 feature의 변경으로 얻어지는 변화는 명확하지 않다.)
• 현실에서 충분히 일어날 수 있는 변경이여야 한다. (본인이 어떠한 변화가 일어나면 병에 걸릴지 알아볼 때 성별 feature를 건드릴 순 없다)

3.4.2 counterfactual explanation의 장/단점

• 장점 : feature 값의 변화에 따라서 예측 결과가 변경되는 것이기 때문에 명확한 원인을 파악할 수 있다.
• 단점 : Rashomon effect, 여러 counterfactual explanation이 동일한 결과를 가질 수 있다.
            (음성에서 양성으로 변하기 위해서 수십가지의 방법이 있을 수 있다.)

이에대해서 자세히 설명한 블로그 주소를 첨부한다. ((Explainable AI) Counterfactual Explanations)