Kernel Method(Feature Mapping, Kernel, Kernel Trick)

1. Mapping Functoin을 통한 새로운 Feature Map 생성

기존에 주어진 \(Feature \ Space \ X\)가 문제를 Linear 한 방법으로 해결이 불가능할 경우,

새로운 \(Feature \ Space \ \phi(X)\)를 만들어 해결할 수 있으며, 이때 사용되는 \(\phi(X)\)를 Mapping Function이라고 한다.

이에 대한 예시는 아래와 같다.

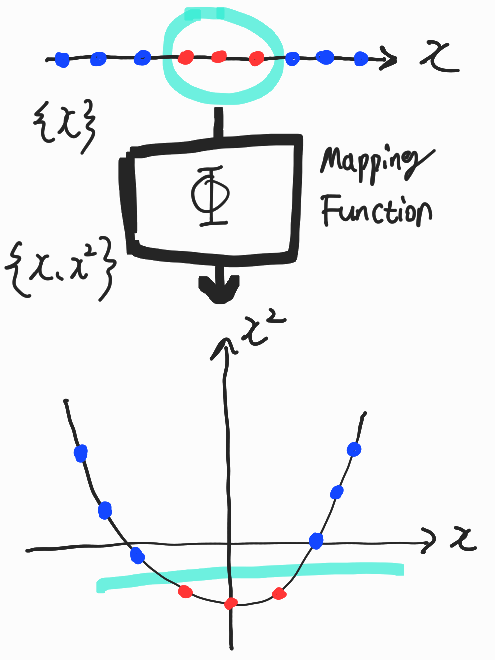
그러나 어려움이 있으니.

1. 적절한 Mapping Function을 찾기 어려움

2. 기존 \( x_{i}^{T}x_{j}\) 비해서 \( \Phi(x_{i})^{T}\Phi(x_{j}) \)는 많은 연산량이 요구

    (데이터의 컬럼 수가 증가하기 때문에 내적 연산량의 증가)

 

2. Mapping Function을 통한 계산과정

두개의 컬럼으로 이루어진 데이터셋 X가 있을때 임의의 두점 A,B를 뽑았다고 가정한다.

$$  A = \begin{pmatrix}3 \\1\end{pmatrix},B = \begin{pmatrix}2 \\2\end{pmatrix}  $$

그리고 Mapping Function은 아래와 같다.

$$  \Phi(X) = (x_{1}^{2}, x_{2}^{2}, \sqrt{2}x_{1}x_{2}) $$

두 점 A,B에 Mapping Function을 적용하면 아래와 같다.

$$ \Phi(A) = \begin{pmatrix}9\\1\\3\sqrt{2}\end{pmatrix}\,\Phi(B) = \begin{pmatrix}4\\4\\4\sqrt{2}\end{pmatrix}  $$

이를 실제 계산해보면 64의 값이 나오며, 과정은 아래와 같다.

3. 동일한 결과를 내는 어떠한 Kernel Function 찾기

다음과 같은 Kernel이 정의되어 있다고 한다.

$$ K(A,B) = (A \cdot B)^{2} $$

해당 Kernel을 사용해서 위의 A,B에 대해 계산해보면 아래와 같다.

위의 Mapping Functoin이 비선형 문제를 선형으로 표한할 수 있는 적절한 Mapping Functoin이었다면,

우리는 동일한 결과를 내는 Kernel Function을 찾아낸 것이다.

실제 Kernel Function을 구할때는 Mercer's theorem을 만족해야하며, 본 포스팅에서는 해당 내용을 다루지 않는다.

 

4. Kernel Trick(or Kerenl Substitution)

어떠한 수식이 백터의 내적을 포함하고 있을 때, Kernel Function으로 대치하여 계산하는 것을 Kernel Trick이라고 한다.

우리는 Kernel Trick을 통하여 적절한 Mapping Function을 찾는 어려움과 많은 내적 연산량을 해결할 수 있다.

(이미 검증된 다양한 Kernel Function들이 나와있다.)

 

SVM에서의 Mapping Function 및 Kernel Trick이 적용되는 과정을 수식으로 나타내면 아래와 같다.

5. Kernel Trick 종류

추후 기술 예정