-
최대우도법(Maximum Likelihood Estimation, MLE)Data Science/데이터마이닝 2022. 11. 3. 23:42반응형
어떠한 예측 모델을 만들때 생성된 모델이 얼마나 Train data set을 잘 설명하는지를 측정할 필요가 있으며, 이를 좋은 방향으로 개선해나아감으로 모델을 학습할 수 있다.
Train data set에 대한 설명력을 측정하는 가장 대표적인 방법으로는 손실함수(Loss function)가 있다.
다른 방법으로는 이번 포스팅에서 설명할 Likelihood가 있다.
1. Likelihood란?
X라는 데이터는 자연에서의 True Distribution에서 발생하였다.
이때, 우리는 모집단을 알수 없기 때문에 샘플링 된 데이터를 통해서 True Distribution을 추정해야한다.
따라서 True Distribution일 가능성(Probability)을 Likelihood라고 할 때 가장 높은 가능성을 가지는 분포를 찾는 것을 최대우도법(Maximum Likelihood Method)라고 한다.
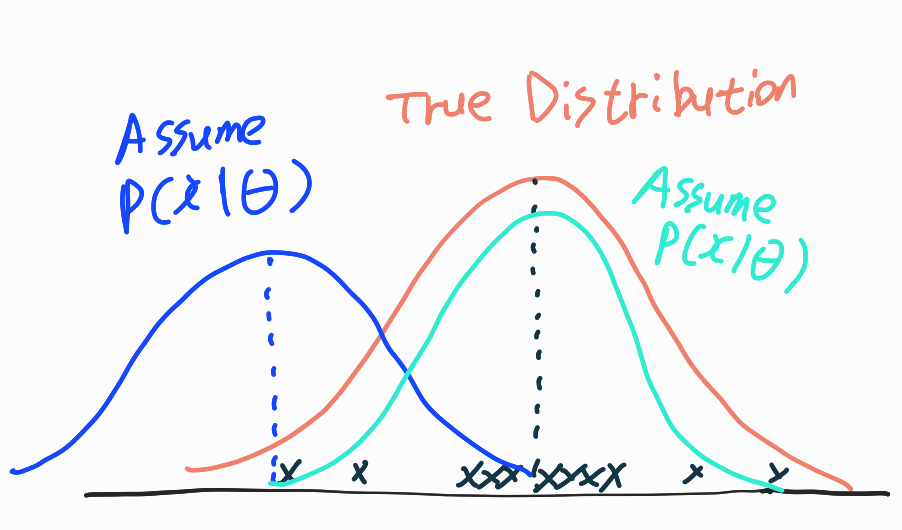
아래의 그림에서는 주황색의 True Distribution이 존재하고 그로부터 샘플링된 데이터(x)가 있다.
이때 파란색 분포와 민트색 분포를 가정할 수 있는데 민트색 분포가 좀더 데이터를 잘 설명한다고 할수 있다.
샘플링된 데이터를 가장 잘 표현하는 분포를 찾기 위해서 가정된 분포에서 샘플링된 데이터가 나타날 가능성(probability)을 모두 곱한다. (곱해주는 이유는 모든 데이터의 추출이 독립적이기 때문이다.)
따라서 데이터 k개가 존재할 때, 모든 데이터가 추정된 분포에서 가지는 likelihood는 아래 수식과 같다.
$$ P(x|\theta)=\prod_{k=1}^{n}P(x_{k}|\theta) $$
곱하기보다는 더하기가 편하기 때문에 log를 씌워서 곱하기를 더하기로 바꾸어준다.
$$ L(\theta|x) = logP(x|\theta) = \sum_{i=1}^{n}logP(x_{i}|\theta) $$
2. Maximum Likelihood
위의 내용들을 기반으로 가장 높은 likelihood를 가지는 분포가 Train data set을 가장 잘 설명하는 분포라고 판단할 수 있다.
따라서 가장 높은 likelihood를 가지게하는 \( \theta \)를 찾아야한다.그 방법은 \( \theta \)에 편미분을 하고 그 값이 0이 되는 \( \theta \)를 찾는다.
$$ \frac{\partial }{\partial \theta}L(\theta|x) = \frac{\partial }{\partial \theta}logP(x|\theta) = \frac{\partial }{\partial \theta}\sum_{i=1}^{n}logP(x_{i}|\theta) = 0 $$
반응형'Data Science > 데이터마이닝' 카테고리의 다른 글
최적화 함수 종류 및 개념(Optimization Function) (0) 2022.11.11 Kernel Method(Feature Mapping, Kernel, Kernel Trick) (0) 2022.11.07 Linear Regression 코드 주석 (0) 2022.10.18 파이썬에서 시간값 다루기 - Datetime, Timedelta (0) 2022.10.07 클러스터링 기법 - 개념, 타당성평가, 종류 (0) 2022.10.05