최적화 함수 종류 및 개념(Optimization Function)

출처: 하용호, 자습해도 모르겠던 딥러닝, 머리속에 인스톨 시켜드립니다(https://www.slideshare.net/yongho/ss-79607172)

1. Gradient Descent(GD, 경사하강법)

함수의 기울기를 구하고 기울기의 반대 방향으로 이동시켜 최소값에 이르를때까지 반복하는 기법.

ML모델의 최적화시에 전체 데이터를 모두 사용하기에 Batch Gradient Descent라고 부르기도 한다.

모든 데이터에 대한 loss를 구해야하기 때문에 많은 연산량을 요구한다.

$$ w_{i+1} = w_{i}-\gamma _{i}\triangledown f(w_{i}) $$
\( \gamma \) : 이동 거리를 조절하는 매개변수, 흔히 Learning rate(학습률)로써 ML분야에서 쓰인다.
\( \triangledown \) : 미분연산자를 의미한다. (nabla, 나블라)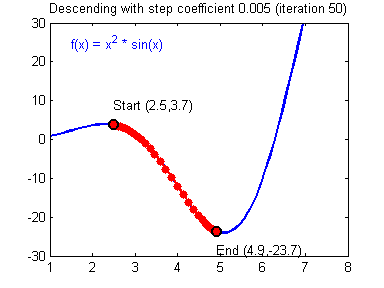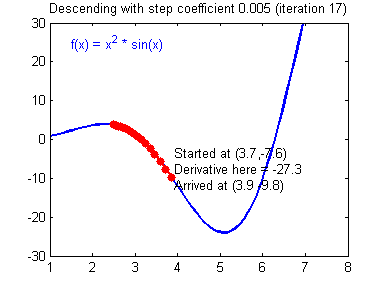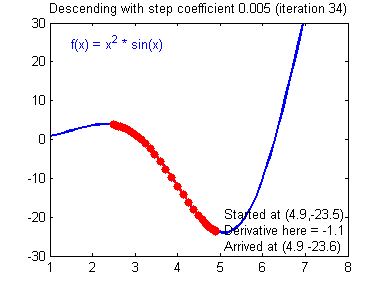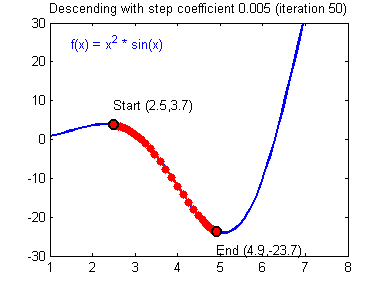

어떠한 함수 \(f(x)\)에서 gradient descent가 동작하는 방법 (출처 : https://hackernoon.com/life-is-gradient-descent-880c60ac1be8)

2. Gradient Descent 종류에서 주의해야할 점

2.1 적절한 이동거리(Learning rate) 설정

경사의 반대방향으로 얼마나 이동할지를 결정하는 Learning rate를 적절히 선정하는 것이 중요하다.너무 작을 경우 : 함수의 최저점으로 이동하는데 상당한 수행 횟수가 필요하다.너무 클 경우 : 함수의 최저점으로 수렴하지 못하고 발산할 수 있다.

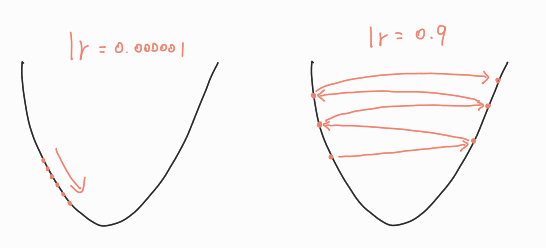
2.2 Local Minima Problem

경사가 0인 경우(미분값이 0인 경우)에는 더이상의 이동이 불가능 하므로, 해당지점을 최저점으로 판단한다.

그러나 해당 지점이 Local Minima이고 또다른 지점에 Grobal Minimum이 존재할 수 있다.

2.3 Saddle Point Problem

2.2의 Local Minima와 비슷하지만 다른 문제이다.

어떠한 평평한 점에 초기값이 놓이게 될경우 어느쪽으로도 이동하지 못하는(경사가 존재하지 않기 때문에) 상황이 발생한다.

이를 말안장 같다고 하여서 Saddle Point라 부른다.

 

3. Stochastic Gradient Descent(SGD, 확률적 경사 하강법)

GD가 전체 데이터에 대해서 loss 및 기울기를 구하여 이동한다면,

SGD는 랜덤 샘플링된 일부 데이터만 사용하여 loss 및 기울기를 구하여 이동하는 방법이다.

ML에서는 일부 데이터(Mini-batch)만을 사용하여 Mini-Batch Gradient Descent라고 부르기도 한다.

수식은 GD와 동일하나 이때 사용되는 데이터가 Mini-Batch임을 명심해야한다.

당연히 Mini-Batch만을 사용하기에 계산속도가  GD에 비해서 빠르다.

$$ w_{i+1} = w_{i}-\gamma _{i}\triangledown f(w_{i}) $$

SGD는 일부 데이터만을 사용하여 가중치(w)를 갱신하기 때문에 GD에 비해서 최적의 해를 찾을 확률은 낮으나 속도면에서 훨씬 빠릅니다.

위의 그림에서 최적의 해를 찾아감에 있어서 GD가 더욱 안정적인 모습을 보이지만,

한번의 이동에서 GD는 전체 데이터를 계산하고 SGD는 일부 데이터만 계산한다는 점을 명심해야합니다.

 

4. Momentum(모멘텀)

기존의 SGD와 같이 데이터에서 기울기를 구하지만 이동하는 방향을 결정할 때 Momentum(관성)의 개념을 추가하였다.

$$v_{i+1} = m*v_{i} + \gamma _{i}\triangledown f(w_{i})$$

$$w_{i+1} = w_{i}-v_{i+1}$$
\(v_{i}\) : i번째 이동에서의 w의 이동거리(이동 벡터)
\(m\) : 관성계수(0.9)
\( \gamma \) : 이동 거리를 조절하는 매개변수, 흔히 Learning rate(학습률)로써 ML분야에서 쓰인다.

5. RMSProp(Root Mean Sqaure Propagation)

기존 AdaGrad(Adaptive Gradient)가 학습이 진행됨에 따라서 Learning rate가 감소하다 0으로 수렴하여 더이상 학습되지 않는 문제점을 개선하기 위해서 등장한 기법이다.

AdaGrad와 동일하게 변수(Feature)별로 Learning rate를 조절하지만 기울기 업데이트 방식에서 차이점을 둔다.

AdaGrad는 동일한 비율로 기울기를 누적하는 반면 RMSProp은 지수이동평균(Exponential Moving Average, EMA)을 활용하여 기울기를 누적한다.

지수이동평균에서의 핵심 내용은 최근의 기울기는 많이 반영하고 먼 과거의 기울기는 조금만 반영하는 점이다.

$$g_{i+1} = \alpha g_{i} + (1-\alpha)(\triangledown f(x_{i}))^{2}$$

$$x_{i+1} = x_{i}-\frac{\gamma_{i}}{\sqrt{g_{i+1}+\epsilon }}\cdot\triangledown f(x_{i})$$

\(g_{i}\) : i번째 이동까지의 기울기 누적 크기
\(\alpha\) : 지수이동평균 업데이트 계수(0.999)
\(\epsilon\) : 분모가 0이 되는것을 방지하는 아주 작은 상수
\( \gamma \) : 이동 거리를 조절하는 매개변수, 흔히 Learning rate(학습률)로써 ML분야에서 쓰인다.

 

6. Adam(Adaptive Moment Estimation)

ML분야에서 가장 보편적으로 사용되는 Adam은 Momentum과 RMSProp의 장점을 결합한 알고리즘이다.

$$\hat{v}_{i}=\frac{v_{i}}{1-m}, \ \hat{g}_{i}=\frac{v_{i}}{1-\alpha}$$
$$x_{i+1} = x_{i}-\frac{\gamma_{i}}{\sqrt{\hat{g}_{i+1}+\epsilon }}\cdot \hat{v}_{i-1}$$
\(m\) : 관성계수(0.9)
\(\alpha\) : 지수이동평균 업데이트 계수(0.999)
\(\hat{v},\hat{g}\) : 학습 초기시에 \(v_{i},g_{i}\)가 0이 되는 것을 방지하기 위한 보정 값
\(\epsilon\) : 분모가 0이 되는것을 방지하는 아주 작은 상수
\( \gamma \) : 이동 거리를 조절하는 매개변수, 흔히 Learning rate(학습률)로써 ML분야에서 쓰인다.

 

 

 

추가해야하는 최적화기법들....

AdaGrad,RAdam, AdamW