K-means Clustering 파이썬 구현하기

해당 글에서는 clustering(클러스터링,군집화)의 대표적 기법인 K-Means를 파이썬으로 구현해본다.

Clustering에 대한 이론적인 부분은 "클러스터링 기법(개념,타당성,평가)" 글을 참고.

1. 데이터 준비

sklearn에서 제공해주는 iris 데이터를 사용한다.

clustering이기에 종속변수를 제외하고 독립변수만으로 데이터프레임을 구성한다.

import pandas as pd
from sklearn import datasets


iris = datasets.load_iris()
X = iris.data
y = iris.target

df = pd.DataFrame(X, columns = iris.feature_names)
print(df)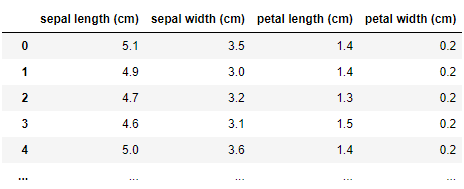

clustering에서는 각 독립변수(컬럼)별로 값의 스케일이 다르면 가지게되는 가중치가 달라진다.

( 독립변수 x1이 1000~10000의 값을 가지고 독립변수 x2가 1~3의 스케일을 가질경우 x1의 변화에 따라서 모델이 좌우되고 x2의 변화는 무시된다.)

따라서 스케일링을 통해서 모든 독립변수간의 스케일을 동일하게 맞추어준다.

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
df.loc[:,:] = scaler.fit_transform(df)

print(df)

2. K-means 생성 및 학습

sklearn의 모든 모델들과 같이 .fit명령어로 학습한다.

clustering은 비지도 학습이므로 독립변수만을 입력으로 받는다.

from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=3, random_state=7)

kmeans.fit(df)

파라미터	기능	초기값	파라미터
n_clusters	cluster 개수 지정	입력필수	정수값
random_state	randomseed 값	None	정수값

분류 결과는 .labels_로 확인가능하다.

print(kmeans.labels_)

새로운 데이터를 학습한 클러스터에 사용할때는 .transform 명령어를 사용한다.

이때 반환되는 값은 주어진 데이터의 값들이 각 cluster와의 거리값이다.

※본 글에서는 별도의 테스트 데이터를 준비하지 않았기때문에 다시한번 데이터프레임을 넣어본다.

distance_df = pd.DataFrame(kmeans.transform(df), columns=["c0", "c1", "c2"])
print(distance_df)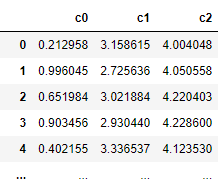

각 cluster의 중앙값은 .cluster_centers_ 명령어로 확인할 수 있다.

centroids = pd.DataFrame(kmeans.cluster_centers_, columns=df.columns)
centroids['cluster'] = ['Cluster {}'.format(i) for i in centroids.index]
print(centroids)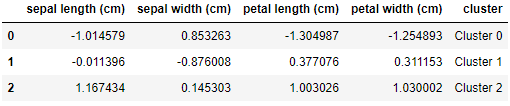

cluster 중심과의 거리 제곱합은 .inertia_ 명령어로 제공된다.

print(kmeans.inertia_)
#=> 140.03275277428648

 

3. 타당성 평가(성능 평가)

Clustering은 정답이 없는 비지도학습이기에 모델의 타당성(또는 성능)을 평가하기위해서 거리값을 사용한다.

또한, cluster 개수별로 타당성을 비교해서 최적의 cluster 개수를 구하는데 사용한다.

 

3.1 Elbow method(엘보우 기법)

군집 내 오차제곱합(SSE, sum of squared error)의 합을 군집화의 비용함수로 정의.

군집 수가 늘어날수록 비용함수는 감소함.

이때, 비용함수 감소 기울기가 급격히 줄어드는 부분(더이상 군집을 늘려도 크게 비용이 감소하지 않는 부분)을 최적의 군집수로 판단한다.

KElbowVisualizer 라이브러리를 활용하여 손쉽게 계산 및 시각화를 할 수 있다.

from yellowbrick.cluster import KElbowVisualizer

k=0
kmeans = KMeans(n_clusters=k, random_state=7)
visualizer = KElbowVisualizer(kmeans, k=(1,6), timings=False)
visualizer.fit(df)
visualizer.show()

위 그림에서 군집수 2개가 가장 최상의 군집 개수라고 추천하고 있다.

3.2 Silhouette Index(실루엣 인덱스)

clustering 기법에서 실질적으로 가장 많이 쓰이는 타당성(평가) 지표이다.

개별객체마다 silhouette index 값을 구할수 있으며, 이에대한 평균값을 사용한다.

모든값이 0.5 이상을 가지면 유의하다고 판단한다.

 

a(i) : 객체 i와 객체 i가 속한 cluster 내 다른 객체들간의 거리 평균

b(i) : 객체 i와 다른 군집에 속한 객체들간의 거리평균 중, 가장 최소값을 가지는 군집과의 거리 평균

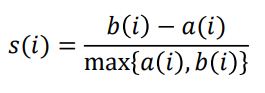
from sklearn.metrics import silhouette_score, silhouette_samples

silhouette_avg = silhouette_score(df, kmeans.labels_)
print(silhouette_avg)
#=>0.3459012795948779

 

cluster 개수별로 silhouette index를 계산하여서 가장높은 값을 가지는 cluster 수를 최적의 값으로 본다.

for k in range(2, 6):
    kmeans = KMeans(n_clusters=k, random_state=7).fit(df)
    silhouette_avg = silhouette_score(df, kmeans.labels_)
    print(f'cluster : {k} // silhouette index {silhouette_avg}')

위의 결과에서는 cluster 2개에서 가장 높은 index 값을 가졌으므로 2가 가장 유의한 cluster 개수라고 할 수 있다.

이에대한 시각화를 추가하면 아래와 같다.

import matplotlib.pyplot as plt
import numpy as np

for k in range(2, 6):
    fig, ax = plt.subplots(1, 1)
    kmeans = KMeans(n_clusters=k, random_state=7).fit(df)
    silhouette_vals = silhouette_samples(df, kmeans.labels_)
    y_ticks = []
    y_lower = y_upper = 0
    for c_num in np.unique(kmeans.labels_):
        cluster_silhouette_vals = silhouette_vals[kmeans.labels_==c_num]
        y_upper += len(cluster_silhouette_vals)
        cluster_silhouette_vals.sort() # numpy array는 sort 메소드를 이용하면 오름차순으로 정렬된 형태로 바뀜
        
        ax.barh(range(y_lower, y_upper), cluster_silhouette_vals, height=1)
        y_lower += len(cluster_silhouette_vals)

0.5 이하의 값들이 존재하므로 해당 clustering은 유의하지 않다고 판단된다.