서포트 벡터 머신(SVM,Support Vector Machine) 파이썬 구현하기(cvxpy, sklearn

1. 개념

SVM은 단순히 A or B 와 같이 class만을 비교하는 Perceptron 모델을 개량한 모델로,

분류선과 데이터간의 거리값(margin)을 최대화하여 분류 강건성을 높였다.

아래 그림에서는 분류선이 초록색 실선으로 나타나며, 양/음의 최대거리값(Maximized margin)의 경계선이 초록색 점선으로 나타난다.

경계선 내부에 찍혀있는 점은 이상치로써, 이를 모두 정상값으로 다루었을 때 강건한 분류선 및 margin이 계산되지 않기 때문에 이상치에 대한 처리도 고려되었다.

2.  cvxpy를 통한 구현

2.1 필요 라이브러리 호출

import cvxpy as cvx
import numpy as np
import matplotlib.pyplot as plt

2.2 사용할 2차원 데이터 랜덤 생성

# 100개의 데이터를 컬럼벡터로 생성
x1 = 8*np.random.rand(100, 1)
x2 = 7*np.random.rand(100, 1) - 4

print(x1.shape, x2.shape)
#=> (100, 1) (100, 1)
# x1,x2를 직접 찍어보는 것도 추천합니다.
# print(x1)

2.3 데이터의 Class값 생성 준비

앞서 랜덤으로 생성된 데이터셋은 class(라벨 또는 정답값)을 가지고 있지 않다.

SVM은 지도학습이기때문에 데이터에 class 정보가 주어져야한다.

따라서 우리는 임의의 선 g(x)를 하나 만들어서 특정 값을 얻고 이를 통해서 class를 배정해줄 예정이다.

※ 이때 사용하는 g(x)는 후에 학습되는 모델과 무관하다.

$$ g(x) = 0.8x_{1} + x_{2} - 3 $$

위의 식을 사용해서 모든 데이터에 대해서 g(x)값을 계산하여 g에 저장한다.

뒤의 2.4에서 g의 값이 1이상일경우 groupA, -1이하일경우 groupB에 배정할 것이다.

# g(X)식 생성 및 계산
# x1, x2는 numpy array이기때문에 g에는 x1,x2의 100개의 값들이 계산된 결과 100개가 들어있다.
g = 0.8*x1 + x2 - 3
print(g.shape)
#=> (100,1)

2.4 Class 배정 및 데이터셋 생성

2.3에서 계산한 g(x)값을 통해서 데이터에 class를 배정한다.

g(x)를 통해서 값이 1 이상인 경우(groupA)와 -1이하인 경우(groupB)로 class를 각각 배정하며, 양측에 속하지 않는 경우는 버린다.

# 조건에 대당하는 값의 인덱스 추출하기
# 여기서 인덱스란 원본데이터 x1,x2에서의 인덱스를 의미함
groupA_idx = np.where(g >= 1)[0] # g(x)의 결과가 1 이상인 데이터들의 인덱스값 추출
groupB_idx = np.where(g <= -1)[0] # g(x)의 결과가 -1 이하인 데이터들의 인덱스값 추출
print(groupA_idx.shape, groupB_idx.shape)
#=> (42,) (58,)
# groupA에는 42개, groupB에는 58개의 데이터가 배정

# 두 그룹의 데이터 개수 측정(또는 길이)
groupA_cnt = groupA_idx.shape[0] # len(groupA_idx) 도 동일한 결과 도출
groupB_cnt = groupB_idx.shape[0]
print(groupA_cnt, groupB_cnt)
#=> 42 58

# 두 그룹에 해당하는 값을 모아 데이터 만들기
# 원본 데이터가 두개의 값을 가지는 2차원 데이터였기 때문에 편향(bias)를 포함한 세개의 값이 들어감
groupA_data = np.hstack([np.ones([groupA_cnt,1]), x1[groupA_idx], x2[groupA_idx]])
groupB_data = np.hstack([np.ones([groupB_cnt,1]), x1[groupB_idx], x2[groupB_idx]])
#=> (42, 3) (58, 3)

# np.ones([groupA_cnt,1])는 주어진 차원만큼 1로 채워진 array를 생성한다.
# print(np.ones([groupA_cnt,1]).shape)
# => (42, 1)

# 이상치에도 강건한지 보기위하여 임의의 이상치를 생성한 후 groupA에 삽입
print('이상치 추가전 : ',groupA_data.shape)
outlier = np.array([1, 2, 2]).reshape(1,-1)
groupA_data = np.vstack([groupA_data, outlier])
print('이상치 추가후 : ',groupA_data.shape)
#=>이상치 추가전 :  (42, 3)
#=>이상치 추가후 :  (43, 3)

# groupA_cnt 갱신
groupA_cnt = groupA_data.shape[0]

# 두 데이터를 매트릭스 형태로 변환
groupA_data = np.asmatrix(groupA_data)
groupB_data = np.asmatrix(groupB_data)

# GroupA,B를 합쳐서 종합 데이터 만들기
total_data = np.vstack([groupA_data, groupB_data])

# 종합 데이터의 class값을 가지는 정답값 만들기
# groupA는 1, groupB는 -1로 class 배정
y = np.vstack([np.ones([groupA_cnt,1]), -np.ones([groupB_cnt,1])])

# 총 데이터의 데이터 개수 측정(또는 길이)
total_cnt = groupA_cnt + groupB_cnt
print(total_cnt)
#=> 101

2.5 cvxpy를 통한 SVM 모델 구현

SVM 모델은 최대의 Margin을 가지도록 학습한다.

아래는 Margin의 수식이다.

$$ margin = \frac{2}{\left\|\omega \right\|_{2} } $$

\(\left\|\right\|\)는 L2_norm(또는 유클리디언거리)를 의미한다.

이때, 무언가의 최대값을 구하는것보다 최소값을 구하는 것이 수학적으로 쉬우므로 margin의 분모인 \(\left\|\omega \right\|_{2} \)의 최소값을 구하는 문제로 변경하여 계산한다.

 

그러나, 데이터에 이상치가 있을경우 최대값의 Margin 구하는데 나쁜영향을 줄수 있다.

아래 그림에서 이상적인 분류선은 회색선이지만, 이상치(초록점선에 근사한 파란점)하나로 인해서 분류선이 크게 변경된 것을 볼수 있다.

이상치에 휘둘리지 않는 강건한 분류선을 그리기 위해서 일부의 오분류(Margin의 범위 내에 값이 존재하는 상황)를 허용하기로 하였다.

단, 허용하는 오분류를 최소화하기 위해서 오분류되는 값을 정분류로 바꾸는데 필요한 보정값(class A : u, class B : v)를 정의하고 최소화한다. (\(u \ni \left\{u_{1},u_{2},...,u_{n} \right\}\))

(사실 보정값보다는 허용오차가 더 정확한 개념이다.)

기존의 정분류 값은 u(또는 v)가 0일 것이고 오분류값은 이상정도가 심할수록 높은 양의 정수를 가지게 된다.

 

위의 두가지 케이스를 고려하는 최소화 수식은 아래와 같다.

$$minimize \ \left\| \omega\right\|_{2} + \gamma \left ( 1^{T}u + 1^{T}v \right )$$

\(\left\| \omega\right\|_{2}\)에서는 margin의 최대화를 의미하며,

\(1^{T}u + 1^{T}v\)에서는 오분류의 최소화를 의미한다.

\(\gamma\)의 경우 margin 최대화와 오분류 최소화에 대한 비중을 어떻게 할지 결정하는 계수이며 사용자가 직접 정의해줘야하는 하이퍼파라미터이다.

# margin 최대화와 오분류 최소화에 대한 비중을 정하는 하이퍼파라미터
gamma_v = 2

# 수식에서 margin의 거리분모의 값인 w와 보정값(허용오차)값인 d를 cvx 문법에 맞게 생성
w = cvx.Variable([3,1]) # 데이터 2차원 + bias이기에 3 지정
d = cvx.Variable([total_cnt,1]) # 모든 데이터가 보정값(허용오차)를 가지기에 total_cnt만큼 생성

# 최소화 수식에 맞추어 cvx.Minimize 식 작성
obj = cvx.Minimize(cvx.norm(w,2) + gamma_v*(np.ones([1,total_cnt])*d))

# 포스팅에서는 생략되었지만, 각 값들이 가져야하는 제약조건 삽입
const = [cvx.multiply(y, total_data*w) >= 1-d, d >= 0]

# 모델 학습
# 이때 margin 최대거리를 나타내는 w값은 자동 갱신
prob = cvx.Problem(obj, const).solve()

# w 값 추출
w = w.value
print(w)
#=> [[-11.4003159 ]
#    [  3.02112189]
#    [  3.82195472]]

2.6 SVM 결과 시각화

# 분류선을 그리기 위한 더미값 생성
# 점을 여러개 겹쳐서 찍으면 선이된다.
xp = np.linspace(-1,9,100).reshape(-1,1) # x축 값
yp = - w[1,0]/w[2,0]*xp - w[0,0]/w[2,0] # cvx에서 계산된 w값 기반 g(x)값 - 초록실선
ypt = -0.8*xp + 3 # 이상적인 g(x)값 - 회색실선

plt.figure(figsize=(10, 8))
plt.plot(groupA_data[:,1], groupA_data[:,2], 'ro', alpha = 0.4, label = 'groupA')
plt.plot(groupB_data[:,1], groupB_data[:,2], 'bo', alpha = 0.4, label = 'groupB')
plt.plot(xp, ypt, 'k', alpha = 0.1, label = 'True') # 이상적 분류선 - 회색실선
plt.plot(xp, ypt-1, '--k', alpha = 0.1) # 이상적 분류선 under boundary - 회색점선
plt.plot(xp, ypt+1, '--k', alpha = 0.1) # 이상적 분류선 upper boundary - 회색점선
plt.plot(xp, yp, 'g', linewidth = 3, label = 'SVM') # 계산된 분류선 - 초록실선
plt.plot(xp, yp-1/w[2,0], '--g') # 계산된 분류선 under boundary - 초록점선
plt.plot(xp, yp+1/w[2,0], '--g') # 계산된 분류선 upper boundary - 초록점선
plt.title('Support Vector Machine (SVM)', fontsize = 15)
plt.xlabel(r'$x_1$', fontsize = 15)
plt.ylabel(r'$x_2$', fontsize = 15)
plt.legend(loc = 1, fontsize = 12)
plt.axis('equal')
plt.xlim([0, 8])
plt.ylim([-4, 3])
plt.show()

추가적으로, 본 포스팅에서는 두 그룹이 나누어지는게 명확히 보이도록 g(x)의 값이 [-1,1]인 데이터들은 버렸다.

# 2.3 참고
# groupA_idx = np.where(g >= 1)[0]
# groupB_idx = np.where(g <= -1)[0]

 

위의 조건을 아래와 같이 바꿀경우 그려지는 그래프는 다음과 같다.

# groupA_idx = np.where(g >= 0)[0]
# groupB_idx = np.where(g < 0)[0]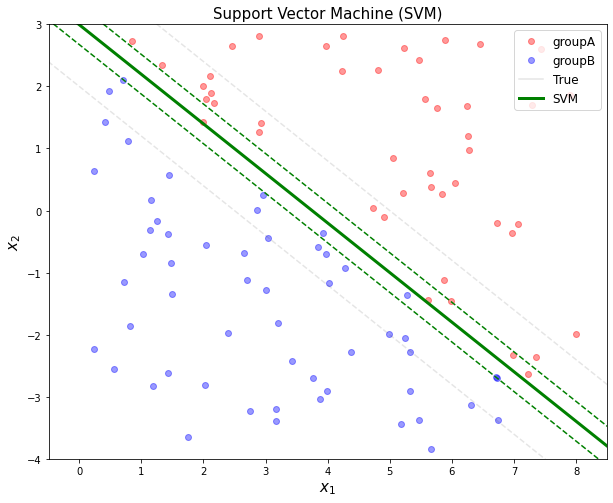

3. sklearn을 통한 SVM 모델 구현

추후 작성 예정