Diffusion Model 기본 개념 공부하기

 

Stable Diffusion이 선보인지 2년이 지난 지금.

뒤늦게나마 해당 모델에 대해서 공부를 시작하려한다.

그 첫번째로 오늘은 Diffusion Model의 개념에 대해서 공부해본다.

 

관련 자료들을 찾아가며 공부한 내용을 정리한 포스팅으로

잘못된 풀이나 정보에 대한 피드백은 언제나 감사히 받겠습니다.

1. 생성형 모델

 

생성형 모델은 입력받은 데이터와 유사한 분포를 따르는 새로운 데이터를 생성하는 모델이다.

즉, 데이터의 분포를 학습 한다고 할 수 있다.

기존의 대중적인 생성형 모델로는 GAN, VAE, Flow-based model이 있으며,

모두가 데이터의 분포를 학습하는 모습을 볼 수 있다.

 

GAN : Generator가 주어진 latent vector로부터 실제(데이터)와 최대한 유사한 임의의 데이터를 생성한다.
Discriminator가 Generator의 결과를 판단하며 서로 상호작용해 학습해나간다.

VAE : Decoder는 Encoder로부터 압축된 저차원 latent vector를 다시 고차원의 원본 데이터로 복원한다.

Flow-based model : f(x)로부터 얻어지는(flow) 고차원의 확률 분포(z)를 비교적 간단히 확률분포로 근사(inverse)하여, 복잡한 확률 분포 p(x)를 모델링 하는 것이다.

 

https://lilianweng.github.io/posts/2021-07-11-diffusion-models/

 

2. Diffusion Model 기본 개념

 

그렇다면 Diffusion Model은 어떠한 개념일까?

원본 데이터(\( x_0 \))에서 T번 만큼 단계적으로 노이즈를 추가하여 확산된(diffusion) 값(z)를 가지게 한다.

이후 값(z)으로부터 T번 만큼 단계적으로 노이즈를 제거하면 다시 원본 데이터(\( x_0 \))를 얻을 수 있다는 개념이다.

 

https://arxiv.org/pdf/1503.03585.pdf

 

3. Forward Diffusion Process, 어떻게 노이즈를 주는가?

 

\( x_0 \) 로부터 \( x_ T \)(또는 z)까지 노이즈를 주는 과정을 Forward Diffusion Process 라고 지칭한다.

먼저, 아래의 그림을 본 이후 마저 설명을 진행하겠다.

(해당 그림은 고려대 산공 DSBA 연구실의 유튜브에서 가져왔는데 아주 설명이 잘 되어있다.)

 

https://www.youtube.com/watch?v=_JQSMhqXw-4

 

우리가 먼저 살펴보아야 할 부분은 이것이다.

 

 

이전의 상태(\( x_{t-1} \))에서 다음의 상태(\( x_t \))로 넘어갈 때 항상 사전에 정의된 값 만큼의 노이즈가 주입된다.

사전에 정의된 값은 β로 나타나는데, \( {\beta}_0 \) 부터 \( {\beta}_T \) 까지의 값은 일정할 수도 특정 함수(시그모이드 등)를 따를 수도 있다.

 

https://ko.wikipedia.org/wiki/%EC%8B%9C%EA%B7%B8%EB%AA%A8%EC%9D%B4%EB%93%9C_%ED%95%A8%EC%88%98

 

이제 T번만큼 β가 주입된다는 것을 알았다.

과연 어떻게 주입되는지에 대해서도 자세히 알아보자.

 

원본 논문 15페이지에서 그 수식을 찾을 수 있다.

※ 평균 및 분산 기호가 있으면 좋을 것 같아 유튜브 수식도 가져왔다.

 

https://arxiv.org/pdf/1503.03585.pdf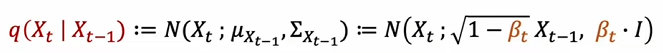

https://www.youtube.com/watch?v=_JQSMhqXw-4

 

\( x_{t-1} \)에서 \( x_{t} \)로 가는 확률분포는 \( x_{t-1} \) 의 평균과 분산을 가지는 가우시안 분포(N)이다.

하지만, 노이즈를 포함하게 된다면 평균값이 \(  \sqrt{1-\beta_t} X_{t-1} \)이고 분산이 \( {\beta}_t \)인 가우시안 분포를 가지게 된다.

여기서 짚고 넘어가야할 것은 \( x_{t-1} \)에서 \( x_{t} \)로 갈때 확률분포이기 때문에 항상 같은 값을 가진다고 보장할 수 없다.

 

이는 아래의 코드를 보면 더욱 이해가 쉽다.

 

https://www.youtube.com/watch?v=_JQSMhqXw-4

 

기존값( \(  x_{t-1} \) )에  \( \sqrt{1-\beta_t} \)만큼을 곱하고

가우시안 분포에 따라서 생성돈 노이즈에 \( \sqrt{\beta_t} \)  를 곱한 후 

서로 더해준 값이 \( x_t \) 이다.

 

torch.rand_like는 가우시안 분포(정규분포)를 따름을 아래 공식문서에서 알 수 있다.

 

https://pytorch.org/docs/stable/generated/torch.randn_like.html

 

 

이렇게 우리는 T번의 반복을 통해 \( x_0 \)로부터 노이즈를 단계적으로 주어

\( x_T \) 즉, z를 만들었다.

 

4. Marcov 적 특성

 

자, forward process를 모두 이해했다면,

이제는 Marcov 특성을 한번 짚고 넘어가야한다.

뒤의 Backward process에서는 해당 개념을 알아야하기 때문!

 

간단하게만 요약하자면,

과거의 과정을 모두 무시하고 현재의 상태만이 이후의 상태에 영향을 미친다는 의미이다.

 

각각의 확률 분포에 따라서 \( x_0 \) 부터 \( x_{t-1} \)까지 왔지만,

\( x_{t} \) 에는 오직 \( x_{t-1} \) 만이 영향을 미친다는 의미이다.

 

앞서 사용한 식에서도 자명한 것이

xt를 구할 때 오직 \( x_{t-1} \) 과 \( {\beta}_t \) 만이 사용되었다. ( \( x_{t-2} \) 사용 안됨)

 

https://arxiv.org/pdf/1503.03585.pdf

 

5. Reverse Diffusion Process, 어떻게 노이즈를 제거하는가?

 

Reverse diffusion preocess의 개념은 간단하다.

 

Forward diffusion process에서의 각 단계별로 적용된 계산을 z로부터 역으로 계산해나가면 다시 원본의 \( x_0 \)를 얻을 수 있다.

즉, 조건부 확률 \( q(x^t|x^{t-1}) \) 로 계산된 값이기에 \( q(x^ {t-1} |x^t) \) 를 알 수 있으면 역계산도 할 수 있다는 의미이다.

 

하지만!!

우리는 각 단계(t시점)에서 사용된 확률분포 \( q(x^t) \) 를 알 수 없기에 계산이 불가능하다.

 

그렇기에 등장하는 것이 근사 함수 \( p_{\theta} \left ( X_{t-1} | X_t \right ) \) 이다.

 

확률분포 \( q(x^t) \)를 알 수는 없지만,

각 단계에서 생성된 \( x^t \) 와 \( x^{t-1} \)을 알고있기에,

이를 활용하여 근사한 \( p_{\theta}(X_{t-1}|X_t) \)를 학습시킬 수 있다.

 

즉,

\( p_{\theta} \left ( X_{t-1} | X_t \right ) \)  \( \approx \) \( q \left ( x_{t-1} | x_{t} \right ) \)  이다.

 

이렇게 학습된 모델은

관측된 값 \( x^t \) 과 학습된 확률분포 \( p_{\theta} \) 간의 근사함을 계산하며,

이에 대해서 자세히 나타낸 예시는 아래와 같다.

 

https://www.youtube.com/watch?v=_JQSMhqXw-4

 

Regularization에서 \( x_0 \) 으로부터 \( z \)까지의 확률분포가 잘 근사되었는지를 반영한다.

Denoising Process에서 각 단계에서 ( x_{t} \) 에서 ( x_{t-1} \)으로 복원하는 확률분포가 잘 근사되었는지 반영한다.

Reconstruction에서 likelihood의 최대값을 통해 얼마나 \( x_0 \)가 잘 복원되었는지를 반영한다.

 

이때 Reconstruction은 likelihood 개념을 사용하지만 Regularization 와 Denoising Process는 KL-divergence를 사용한다.

KL-divergence는 두 확률분포의 차이를 계산하는 식을 의미한다.

 

 

 

참고문헌

원본논문
https://arxiv.org/pdf/1503.03585.pdf
[Paper Review] Denoising Diffusion Probabilistic Models
https://www.youtube.com/watch?v=_JQSMhqXw-4
초보를 위한 정보이론 안내서 - KL divergence 쉽게 보기
https://hyunw.kim/blog/2017/10/27/KL_divergence.html