강화학습(Reinfocement Learning) 정의 및 개념

1. 강화학습(Reinfocement Learning)이란

강화학습이란 Cumulative reward 를 높이기 위해, 특정 환경에서 intelligent agent 가 어떤 action 을 취해야하는 지 연구하는 분야이다. (최적의 policy 찾기)

지도학습이 모델에게 독립변수(x)와 종속변수(y)를 제공하고 학습한다면,

강화학습은 모델에게 state(s)와 reward(r)을 제공하고 학습한다.

 

강화학습은 아래의 경우 사용하면 좋다.

• 각 state에 대해서 최적의 행동(optimal action)이 뭔지 모를 때
• 과정을 모르고 결과에 대한 Reward만 정해줄 수 있을 때
• 여러 시도 및 실패 과정을 거처도 될 때

강화학습을 그림으로 나타내면 아래와 같다.

 

 

Agent는 Environment의 어떠한 State에서 어떠한 Action을 취함으로써 Reward를 받는다.

(Action에 따라서 State는 갱신된다.)

위의 내용을 수식으로 표현하면 아래와 같다.

$$ f:(s_{t},a_{t})->(s_{t+1},a_{t+1}) $$

 

1.1 Policy(정책)

특정 state에 따라서 action을 반환하는 함수

• Deterministic policy

• Stochastic policy

 

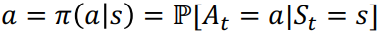
1.2 Value functions

State s 또는 (State s, Action a)를 평가하는 함수

• State value function V

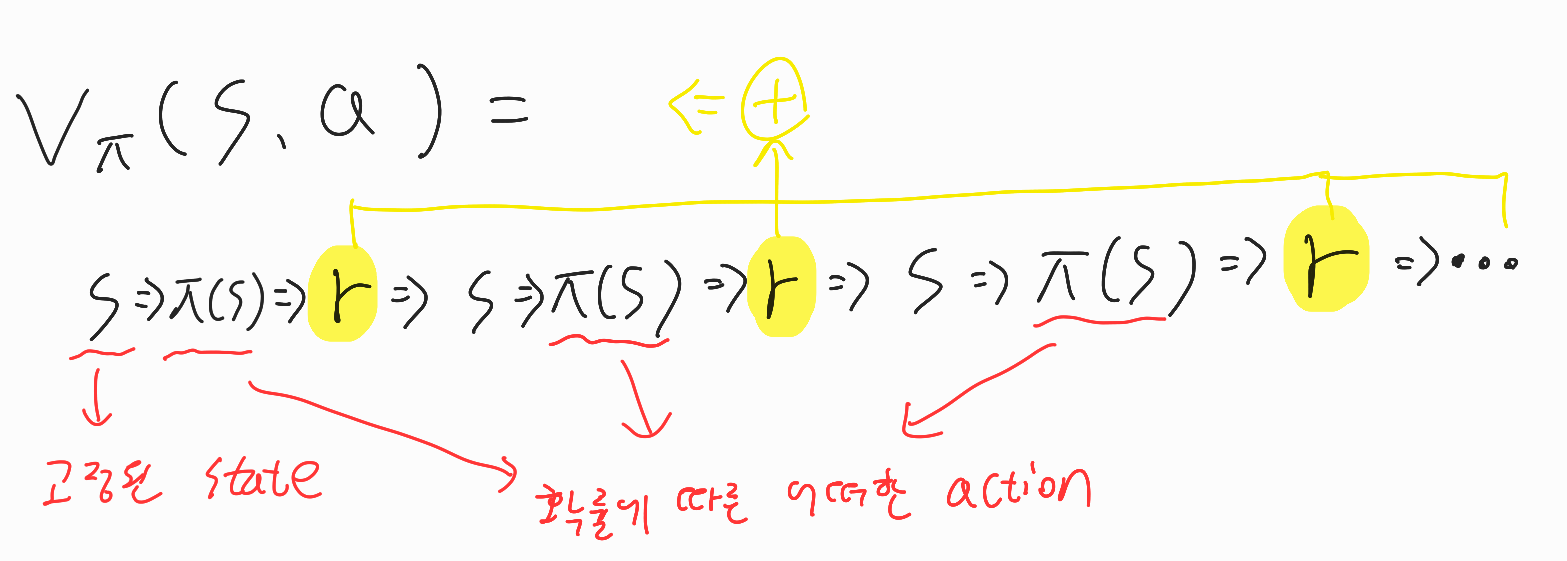
※실제로는 \(\pi(s)\)에서 여러 분기가 나올 수 있다.

• Action value function Q

※실제로는 \(\pi(s)\)에서 여러 분기가 나올 수 있다.

 

\( Q_{\pi}(s,a) > V_{\pi}(s,a) \) 일경우 state s에서는 \(\pi(s)\) 보다 특정 actoin a를 선택하는 것이 더 좋은 상황임을 의미한다.

1.3 Exploration and Exploitation

Exploration : 현재의 best보다 더 나은 결과를 얻을지도 모르기때문에 샘플링 되지 않은 것을 시도한다. (try under-smapled)

Exploitation : 충분한 근거로부터 보장되는 현재에서의 best를 선택한다.

 

2. Markov Decision Process(MDP)

Markov Decision Process란 Markov Property를 만족하는 <S,A,R,P> process이다.

2.1 Markov Property란?

state t에서 state t+1로 가는 확률과,

state 1부터 state t까지 도달한 후 state t+1로 가는 확률이 동일함을 의미한다.

즉 어떠한 state에서 다음 state로 가는데에 있어서 이전 state에 영향을 받지 않고 오직 현재 state만 가지고 결정이 됨을 의미한다.

2.2 <S,A,R,P> Process란?

• S : state
• A : action
• R : reward
• P : transition kernel \( P(S_{t+1},R_{t+1} | S_{1},A_{1}, ... , S_{t},A_{t}) \)

 

3. Bellman Equation

value function이란 state s혹은 (s, a) 를 평가하는 함수이다.

어떠한 policy에 대한 value function V가 존재할 때 bellman equation을 만족해야하기 때문에,
bellman equation으로 value function을 계산하여 V에 대하여 policy evaluation을 진행할 수 있다.

 

Bellman equation은 value function 을, policy, reward, discounted future value 등으로 분해(decompose) 한 관계식

\( \gamma \)는 discount value를 의미한다.

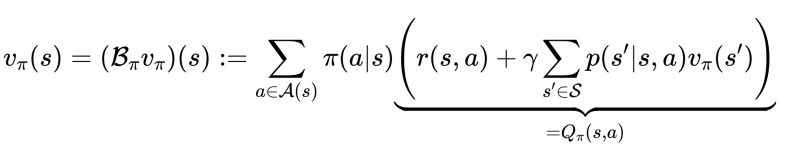
4. Optimal Policy

4.1 Policy Iteration

모든 state와 action에 대한 reward 정보(\(r(s,a)\))를 알고있고, transition dynamics \( P(s'|s,a) \)를 알고있다는 가정하였을 때 최적의 policy를 찾는 방법.

$$\pi_{k+1}(s) = \underset{a\in A(s)}{argmax} r(s,a) + \gamma \sum_{s' \in S}p(s' | s,a)V_{k}(s')$$

알고리즘은 아래와 같으며 각 단계별로 자세히 알아보자.

1) 현재 policy \(\pi\)의 value function V(s)를 구한다. (policy evaluation)

2) value function V(s)을 이용해 greedy하게 최적의 action을 선택하도록 \(\pi\)를 업데이트 한다. (policy improvement)

3) \(\pi\)가 수렴할 때까지, 1~2과정을 반복한다. (policy iteration)

 

4.2 Value Iteration

Value function을 직접 maximize 할 수 있다면 Policy를 계속 갱신하지 않아도 최적의 policy를 찾을 수 있다.

알고리즘은 아래와 같으며 각 단계별로 자세히 알아보자.

1) 현재 policy \(\pi\)의 value function V(s)를 구한다.

 

2) V(s)가 수렴할 때까지, 1과정을 반복한다.

\( \Delta \) : V(s)와 New V(s)의 차이의 절댓값

\( \theta \) : maximize 기준 임계치 ( \( \theta \)가 3일경우 \( \Delta \)가 3 이상일 경우 maximize에 수렴했다고 판단

3) 수렴한 V(s)를 이용해서 \(\pi\)가 최적의 action을 선택하도록 업데이트 한다.

5. value function을 계산하는 여러 알고리즘(정책)

5.1 \(\epsilon - greedy \) 알고리즘

특정확률( \(\epsilon\) )로 랜덤하게 state를 선택하고 나머지 특정확률( \(1-\epsilon\) )로 best state를 선택하는 기법

앞서 1.3에서 설명한 Exploration and Exploitation를 섞어서 쓰는 방식이다.

5.2 Upper Confidence Bound (UCB) 알고리즘

https://shakeratos.tistory.com/100

 

6. Monte Carlo Method(MC)

알지못하는 값을 예측하기 위해 sample된 값의 평균을 사용하는 방법.

sample들이 독립이고 sample의 수가 충분히 많다면, sample의 평균은 실제 값에 수렴한다.

 

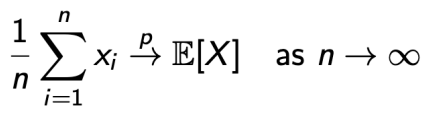
6.1 Monte Carlo Method  vs  Dynamic Programming Method

• Monte Carlo Method
  Environment에 대한 사전 정보가 없어도 된다. 
  반복된 무작위 추출로 실체를 근사하는 방법이다.
  에피소드가 모두 끝난후에 업데이트를 진행한다.
• Dynamic Programming Method
  환경에 대한 정보가 필요하다. 
  매 time step마다 업데이트를 진행한다.

7. Temporal Difference Learning(TD)

Monte Carlo Method와 Dynamic Programming Method의 장점을 섞어서 만든 Method

기존 MC가 샘플링을 통해 얻은 \(G_{t}\)를 이용해 업데이트한다면,

TD는 예측을 통해 얻은 \(R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_{t+1},A_{t+1})\) 값을 이용해 업데이트 한다.

7.0 On-policy vs Off-policy

• On-policy : Target Policy와 behavior policy가 같은 경우
• Off-policy : Target Policy와 behavior policy가 다른 경우

7.1 SARSA(On policy)

직접 해보고 기존의 정책을 평가

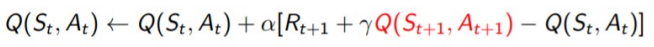
7.2 optimal bellman equation

7.3 Q-learning(Off policy)

해보지 않고 ...

데이터가 정말 충분할 때 수렴

TD-18

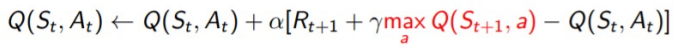
7.4 Double Q-learning

두개로 체크함으로써 maximization bias가 덜 생기게

 

8 n-step Bootstrapping

기존 TD가 근시안적인 단점을 가지고 있었기에

일정 step만큼 참았다가 업데이트를 하겠다는 것

9. Function Approximation

state가 너무 많거나 무한할 경우 이를 dictionary 형태로 저장하기 어렵다.

때문에 이를 대체할 함수를 만들어서 사용한다.

 

00. 기타 지식

 

00.1 Regret

Multi-armed Bandit(MAB)  문제를 푸는 알고리즘들을 평가하는 지표

$$ Regret = 획득 가능한 best reward - 실제 획득한 reward $$

$$ Regret = \mu^{\ast} T - \sum_{i=1}^{K} \mu_{i}E[\tau_{i}(T)]  $$

 

T : 총 실험 횟수

\(\mu^{\ast}\) : 각 arm의 평균 중 최댓값

\(\mu_{i}\) : arm의 기대보상값

\( \tau_{i}(T) \) : T횟수동안  arm i 가 뽑힌 횟수